qwqqqqq
因为太过健忘以至于老是被老师上课殴打,”你怎么能不记得这个激活函数?“。不想再每节课都被鞭尸了TAT。。。。所以还是得写个笔记顺一下我那些混乱的记忆(对手指)
鉴于自己平时调包也没有很关心不同的激活函数对模型有一个什么样的影响,也算是做个小的总结吧,稍微研究一下每个常用的算法里面采用的基本思想、loss和激活函数之间的联系
纯基础科普文,持续更新,那就开始咯
线性回归
线性的模型,只能拟合线性数据。用于回归任务。适用面很窄,但是方便+快
模型基础公式:
激活函数:
就是它本身,恒等映射
损失函数:
它是凸函数,有唯一最小值,一般用MSE(均方误差)
更新参数方法:
最小二乘法(如果特征不是多得离谱的话,一般用这个)
先对参数求偏导
$$ {$$
此时J取得最小值,然后联合求解
梯度下降法
求b同理
逻辑回归
线性的模型,只能拟合线性数据。用于分类。最常用是二分类,方便、快捷。
模型基础公式:
这里的
激活函数:
选用logistic函数,一般用sigmoid
图长这样:
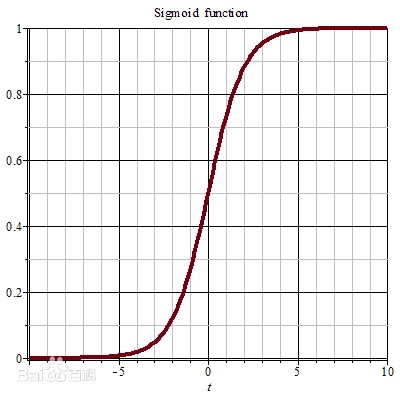
损失函数:
它是凸函数,有唯一最小值,一般用MSE(均方误差)
更新参数方法:
梯度下降法
感知机
线性模型,用于分类。适用面也是很窄的,它是不可导的(因为激活函数不可导)。
模型基础公式:
激活函数:
激活函数用的是阶跃函数
其中
$$
损失函数:
感知机是基于超平面来划分分类的,因此它的误差只考虑误分类点。在误差的选择上,由于sign函数不可导,如果要用梯度来更新参数(求导比较快),我们是没办法选择带
对于损失值的量度,由于感知机的思想是利用超平面来分类,那么我们考虑点到超平面的“距离”来定量。在正确分类的情况下,这个距离是越大越好的,而对于误分类的点来说,它到超平面的“距离”是一个负值,要往增大的趋势(变成正值)走。那“距离”取负值就是我们的损失(因为要最小化损失)。
我这里对”距离“打了双引号,是因为它不同于我们平时所理解的欧氏距离,中间有多一步推导。我这里就省略了,有需要的同学自己去查一下中间那一步推导,还是蛮重要的。得到的距离公式为
假设我们面临的是一个二分类的问题,正类为1,反类为-1。上述公式中,
从公式中也能看出,若分类错误,损失
e.g.若
更新参数方法:
梯度下降法
注意,我们只考虑误分类点。那么对每个误分类点(或随机选取误分类点):
对于每个参数,对损失函数求偏导然后乘学习率作更新。
对误分类点
w:
b:(同理)
更新到训练集没有误分类点,或者误分类点不超过n个(什么约束条件自行设置)就停止。
支持向量机
用于分类,线性的模型,但是可以解决异或问题,同样是超平面的思想,但是是超平面的超进化。这个算法的基本假设是,在低维空间不可分的问题,就把它映射到高维空间,这个高维空间还分不出来就说明维度还不够高,继续去更高维的空间找答案,总有一个维度的空间能线性地解决这个问题。(我愿称之为,最科幻小说的一种算法)
这个算法比较复杂,本人这里也只是做一个简单的概况汇总,很多细节不会细揪,如果是初次学习建议查找其它关于这个算法的资料一起看。
模型基础公式:
其中,
利用核函数对内积作替换,就可以把向量映射到更高维的空间。这里重点介绍一下高斯核函数,因为高斯核函数可以把向量映射到无穷维的空间。其他常用核函数读者可自行查找了解~
高斯核函数:
此模型详细的推导过程可以参考下面这个链接:
激活函数:
跟感知机是一样的
损失函数:
用的函数间隔(距离),跟感知机的思想是一样的,区别点在于,感知机考虑的是每个误分类点距离超平面的距离,而支持向量机是最大化支持向量到超平面的间隔。
定义超平面为:
支持向量到超平面的间隔(距离)为:
目标是最大化这个间隔,根据这条公式一直推导就可以推到模型的基础公式那一条了。详情推导可参考本小节上面那个链接。
然后这里还涉及到了一个优化,使用软间隔(不要求到最优解导致模型过拟合)。引入一个松弛变量的概念对模型划分超平面时做约束,允许部分点被误分类。
使得目标函数变成:
目标是最小化此函数。其中C是一个惩罚系数,C越大,对误分类的惩罚越大,C越小,对误分类的惩罚越小。是一个超参,由用户自己选定C值。
更新参数方法:
序列最小优化算法(类似坐标下降法)
根据基础公式,要求的是
保姆级笔记-详细剖析SMO算法中的知识点 - 知乎 (zhihu.com)
人工神经网络
分类、回归都可以做,非线性模型。由于讲的是基本原理,这里只讲全连接。可以理解为是多个感知机嵌在一起去解决非线性的问题。
模型基础公式:
这个要结合图来理解,每个小圈都是一个神经元,神经元里装着一个数。
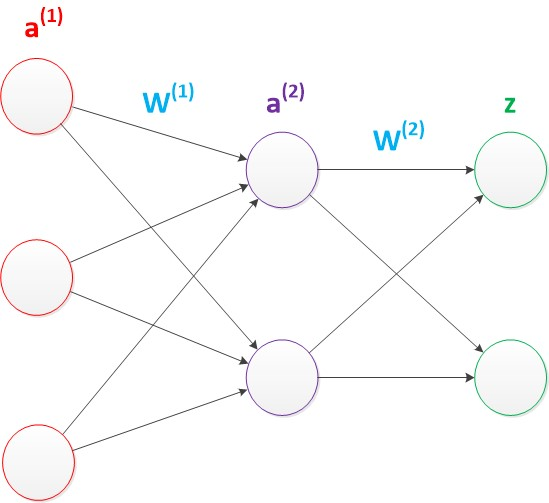
红色这一列是输入层(神经元的个数等于特征长度),紫色的是中间层(隐藏层),可以有很多层,隐藏层的数量、神经元个数,都是用户规定的。绿色的是输出层,神经元个数就是输出的维度,也是由用户设置。每条边的都是一个权重w,从前一层到下一层的过程中,每个下层神经元都是由所有上层神经元*对应权重求和得到的,如果这个下层是中间层,求完和之后还得过一遍激活函数。
说的很抽象,直接看公式吧。先以最上面那个紫色的a为例,并且为了直观理解,暂不考虑激活函数:
其中,每个变量头上那个(k)指的是第k层,
其中,k指第k层神经元,
对最后的输出层,如果这是一个分类任务,还是要套激活函数
激活函数:
隐藏层的激活函数:自行选择,什么都可以,每层都不一样的也可以,但是函数必须可导(后面会说为什么)
输出层的激活函数:
如果这是一个分类任务,用logistic函数,一般选sigmoid(输出概率,取值0-1)
如果是回归任务,选恒等映射
损失函数:
根据不同任务或者自己需求做选择,损失函数要选可导凸函数,保证没有局部最优解,这样用梯度下降法求解就不会陷入局部最优解。
一般分类用交叉熵,回归用MSE。
交叉熵
二分类:y分为0、1两类。
其中,
是模型对第i个输入样本x计算得到的 属于1类的概率。 是第i个样本的标签(0或1),从公式中可以看出损失的计算只考虑自己所属那一类的概率,取log然后取反,损失就变成正的了,如果对正确标签的分类概率越高,那么log(p)就越接近0,损失越小。 多分类:假设y含共M类
其中
详解可以参考这个链接交叉熵损失函数(Cross Entropy Loss) - 知乎 (zhihu.com)
MSE(均方误差)
这个就不用再解释了
参数更新方法:
BP+梯度下降
反向传播(BP):
由于我们选择的激活函数都是可导的,且本来线性的wx+b也是可导的,那么就使得整个大的
反向传播体现在,求导是嵌套的,从最后一层往前求的时候,前层求导会直接用到后层的求导结果,这就使得求导非常方便、速度快。
梯度下降部分,还是老样子:
朴素贝叶斯
用于分类,这是一种生成式算法,从概率的角度出发来解决问题。基本假设是各个特征是相互独立的。
模型基础公式:
推理时,计算每一个label的
基于假设,公式中
其中,j指的是样本
激活函数:
无
损失函数
对数损失函数:
参数求解跟损失函数是不挂钩的,这里只是起一个量化损失的作用,让你看到这个模型的效果如何,算是一种评价指标吧。
参数更新方法:
对训练集的各个特征的频率作统计,作为概率。对每个要被预测的输入,根据输入的特征代公式求解就可以了。
贝叶斯有个点,从公式中也能看出来,一旦训练集确定下来,模型参数的值也就确定下来了,值是唯一的,你重练100次都是这个值。它不像上面的判别式模型那样,用的是随机梯度下降,每次重新训练得到的参数都不一样。
这里还涉及到一个连续型变量的概率统计的问题和输入变量特征不在训练集中的问题。解决的方法是用连续型分布(一般用高斯)去计算概率和做平滑。这里先留个空,之后再填。
暂时写到这里,还有很多很多东西之后再更新(已经累死了
同时这篇文章有点太长了,可能后续会考虑把它拆开或者讲完经典算法之后,把后面新一点的算法换个page写。
